Table of Contents
Introduction to Heaps
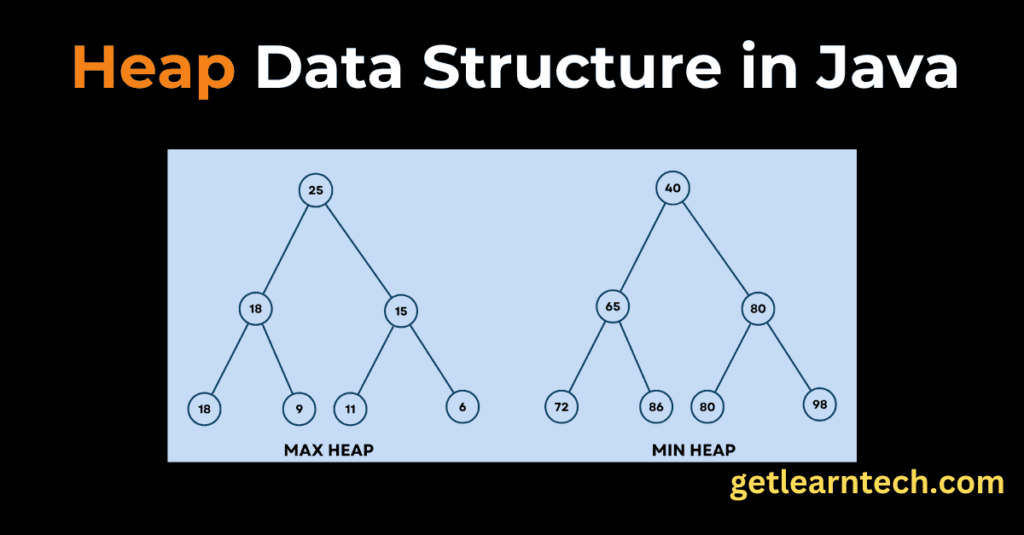
A heap is a specialized tree-based data structure that satisfies the heap property. In a min-heap, for every node i except the root, the value of the parent node is less than or equal to the value of the node i. Conversely, in a max-heap, the value of the parent node is greater than or equal to the value of the node i. Heaps are commonly used in priority queues, graph algorithms, and for implementing efficient sorting algorithms like heap sort.
Types of Heaps
Heap Implementation in Java
- Min-Heap
- In a min-heap, the root node is the smallest element, and every parent node is smaller than its children. This structure is useful when you need quick access to the smallest element. Min-Heap Implementation in Java:
class MinHeap {
private int[] heap;
private int size;
private int maxSize;
public MinHeap(int maxSize) {
this.maxSize = maxSize;
this.size = 0;
this.heap = new int[maxSize + 1];
this.heap[0] = Integer.MIN_VALUE;
}
private int parent(int pos) {
return pos / 2;
}
private int leftChild(int pos) {
return (2 * pos);
}
private int rightChild(int pos) {
return (2 * pos) + 1;
}
private void swap(int fpos, int spos) {
int tmp;
tmp = heap[fpos];
heap[fpos] = heap[spos];
heap[spos] = tmp;
}
private void heapify(int pos) {
if (pos >= (size / 2) && pos <= size)
return;
if (heap[pos] > heap[leftChild(pos)] || heap[pos] > heap[rightChild(pos)]) {
if (heap[leftChild(pos)] < heap[rightChild(pos)]) {
swap(pos, leftChild(pos));
heapify(leftChild(pos));
} else {
swap(pos, rightChild(pos));
heapify(rightChild(pos));
}
}
}
public void insert(int element) {
heap[++size] = element;
int current = size;
while (heap[current] < heap[parent(current)]) {
swap(current, parent(current));
current = parent(current);
}
}
public int remove() {
int popped = heap[1];
heap[1] = heap[size--];
heapify(1);
return popped;
}
}
- Max-Heap
- A max-heap is the opposite of a min-heap, where the root node is the largest element, and each parent node is larger than its children. This structure is beneficial when quick access to the maximum element is required. Max-Heap Implementation in Java:
class MaxHeap {
private int[] heap;
private int size;
private int maxSize;
public MaxHeap(int maxSize) {
this.maxSize = maxSize;
this.size = 0;
this.heap = new int[maxSize + 1];
this.heap[0] = Integer.MAX_VALUE;
}
private int parent(int pos) {
return pos / 2;
}
private int leftChild(int pos) {
return (2 * pos);
}
private int rightChild(int pos) {
return (2 * pos) + 1;
}
private void swap(int fpos, int spos) {
int tmp;
tmp = heap[fpos];
heap[fpos] = heap[spos];
heap[spos] = tmp;
}
private void heapify(int pos) {
if (pos >= (size / 2) && pos <= size)
return;
if (heap[pos] < heap[leftChild(pos)] || heap[pos] < heap[rightChild(pos)]) {
if (heap[leftChild(pos)] > heap[rightChild(pos)]) {
swap(pos, leftChild(pos));
heapify(leftChild(pos));
} else {
swap(pos, rightChild(pos));
heapify(rightChild(pos));
}
}
}
public void insert(int element) {
heap[++size] = element;
int current = size;
while (heap[current] > heap[parent(current)]) {
swap(current, parent(current));
current = parent(current);
}
}
public int remove() {
int popped = heap[1];
heap[1] = heap[size--];
heapify(1);
return popped;
}
}
Binary Heap
A binary heap is a complete binary tree, meaning all levels are fully filled except possibly the last one, which is filled from left to right. Both min-heaps and max-heaps are binary heaps.
Priority Queue
A priority queue is an abstract data type where each element has a priority. Elements are dequeued in order of their priority. Priority queues are often implemented using heaps, as this allows for efficient insertion and deletion.
Using PriorityQueue in Java:
import java.util.PriorityQueue;
public class PriorityQueueExample {
public static void main(String[] args) {
PriorityQueue<Integer> pq = new PriorityQueue<>();
pq.add(10);
pq.add(20);
pq.add(15);
System.out.println(pq.poll()); // Output: 10
System.out.println(pq.poll()); // Output: 15
System.out.println(pq.poll()); // Output: 20
}
}
Heap vs. Stack
The heap and stack are memory areas used in programming languages for different purposes. The stack is used for static memory allocation, storing local variables and function calls. It follows the Last-In-First-Out (LIFO) principle. The heap is used for dynamic memory allocation, where variables are allocated and deallocated in no particular order, allowing for flexible data structures like linked lists and trees.
Heap Sort
Heap sort is a comparison-based sorting algorithm that uses a binary heap. It first builds a max-heap from the input data and then repeatedly extracts the maximum element to sort the array.
Heap Sort Implementation in Java:
public class HeapSort {
public void sort(int arr[]) {
int n = arr.length;
// Build heap (rearrange array)
for (int i = n / 2 - 1; i >= 0; i--)
heapify(arr, n, i);
// Extract elements from heap one by one
for (int i = n - 1; i > 0; i--) {
int temp = arr[0];
arr[0] = arr[i];
arr[i] = temp;
heapify(arr, i, 0);
}
}
void heapify(int arr[], int n, int i) {
int largest = i; // Initialize largest as root
int left = 2 * i + 1; // left = 2*i + 1
int right = 2 * i + 2; // right = 2*i + 2
if (left < n && arr[left] > arr[largest])
largest = left;
if (right < n && arr[right] > arr[largest])
largest = right;
if (largest != i) {
int swap = arr[i];
arr[i] = arr[largest];
arr[largest] = swap;
heapify(arr, n, largest);
}
}
}
Conclusion
Understanding heap implementation in Java is crucial for solving various problems efficiently. Whether you’re dealing with priority queues, implementing heap sort, or comparing heap with stack memory, mastering these concepts can significantly optimize your applications. More Java articles you can explore here.

